队列和双端队列 🔗
双端队列是一种将栈的原则和队列的原则混合在一起的数据结构。
队列 🔗
FIFO(First Input First Output), 先进先出,新添加的元素在队列的尾部,从顶部移除元素。
最常见的例子就是排队。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Queue {
_count: number;
_first: number;
_items: {
[key: number]: any
};
constructor() {
this._count = 0;
this._first = 0;
this._items = {};
}
pop() {
const item = this._items[this._first];
delete this._items[this._first];
this._first++;
return item;
}
push(element: any) {
this._count++;
this._items[this._count] = element;
}
peek() {
if (this.isEmpty()) return undefined;
return this._items[this._first];
}
size() {
return this._count - this._first;
}
isEmpty() {
return this.size() === 0;
}
}
|
双端队列 🔗
是一种允许我们同时从前端和后端添加和移除元素的特殊队列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| class Deque {
_count: number;
_first: number;
_items: {
[key: number]: any
};
constructor() {
this._count = 0;
this._first = 0;
this._items = {};
}
addFront(element: any) {
if (this.isEmpty()) {
this.addBack(element)
} else if(this._first > 0) {
this._first--;
this._items[this._first] = element;
} else {
for (let i = this._count; i > 0;i--) {
this._items[i] = this._items[i-1];
}
this._first = 0;
this._items[this._first] = element;
}
}
addBack(element: any) {
this._count++;
this._items[this._count] = element;
}
removeFront() {
}
removeBack() {
const item = this._items[this._first];
delete this._items[this._first];
this._first++;
return item;
}
peekFront() {
if (this.isEmpty()) return undefined;
return this._items[this._first];
}
peekBack() {
return this._items[this._count];
}
size() {
return this._count - this._first;
}
isEmpty() {
return this.size() === 0;
}
}
|
链表 🔗
普通链表 🔗
链表中的元素在内存中并不是连续放置的。每个元素由一个存储元素本身的节点和一个指向下一个元素的引用(也称指针或链接)组成。

在数组中,我们可以直接访问任何位置的任何元素,而要想访问链表中间的一个元素,则需要从起点(表头
)开始迭代链表直到找到所需的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
| class LinkedList {
head: LNode | null;
equalsFn: Function;
count: number;
constructor(fn: Function) {
this.count = 0;
this.equalsFn = fn;
this.head = null;
}
push(element: any) {
const node = new LNode(element);
this.count++;
if (this.head) {
let current = this.head.next;
while (current?.next) {
current = current.next;
}
current!.next = element;
} else {
this.head = node;
}
}
insert(element: any, position: number) {
if (position >= 0 || position <= this.count) {
if (position == 0) {
const current = this.head;
const insertNode = new LNode(element);
insertNode.next = current;
this.head = current;
return true
} else {
const prev = this.getElementAt(position - 1);
const insertNode = new LNode(element);
const current = prev?.next;
insertNode.next = current;
prev?.next = insertNode;
return true
}
this.count++;
}
return false;
}
getElementAt(index: number) {
if (index >= 0 && index <= this.count) {
let node = this.head;
for (let i = 0; i < index && node; i++) {
node = node.next!;
}
return node;
} else {
return undefined;
}
}
remove(element: any) {
const index = this.indexOf(element);
if (index > -1) {
this.removeAt(index)
this.count--;
}
}
indexOf(element: any) {
if (!element) return -1;
let node = this.head;
for (let i = 0; i < this.count; i++) {
if (node?.node === element) {
return i
} else {
node = node?.next!
}
}
return -1
}
removeAt(position: number) {
if (position < 0 || position > this.count) return
let node = this.head;
for (let i = 0; i <= position; i++) {
node = node?.next!
}
const next = node?.next;
node!.next = next?.next;
}
isEmpty() {
return this.count === 0;
}
size() {
return this.count;
}
}
class LNode {
node: any;
next: LNode | undefined;
constructor(element: any) {
this.node = element;
this.next = undefined;
}
}
|
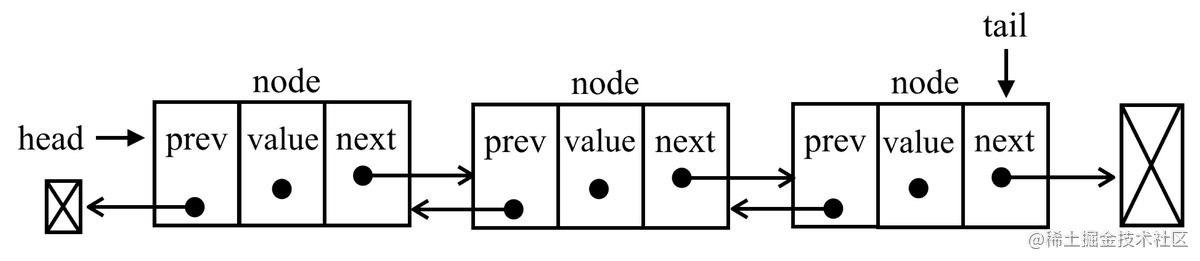
双向链表 🔗
双向链表和普通链表的区别在于,在链表中,一个节点只有链向下一个节点的链接;而在双向链表中,链接是双向的:一个链向下一个元素,另一个链向前一个元素
循环链表 🔗
可以像链表一样只有单向引用,也可以像双向链表一样有双向引用。循环链表和链表之间唯一的区别在于,最后一个元素指向下一个元素的指针(tail.next)不是引用undefined,而是指向第一个元素(head)
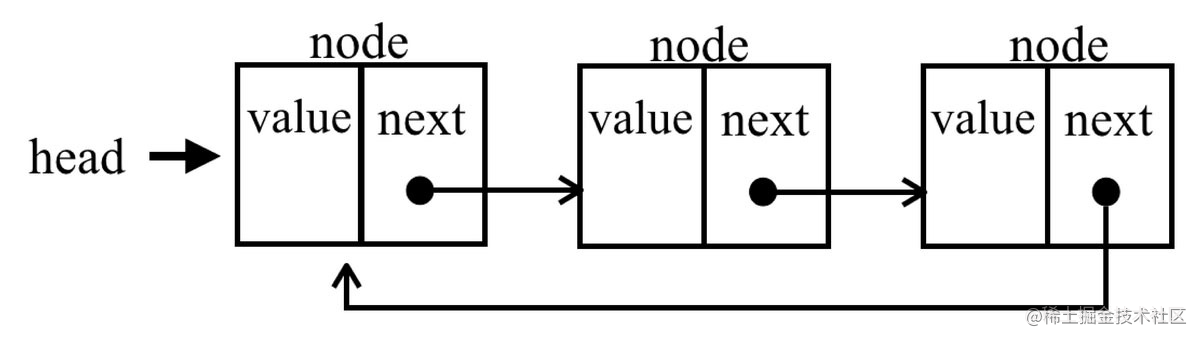
有序链表 🔗
是指保持元素有序的链表结构。除了使用排序算法之外,我们还可以将元素插入到正确的位置来保证链表的有序性
集合 🔗
集合是由一组无序且唯一(即不能重复)的项组成的。该数据结构使用了与有限集合相同的数学概念,但应用在计算机科学的数据结构中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class CSet {
items: any;
constructor() {
this.items = {};
}
add(element) {
if(!this.has(element)) {
this.items[element] = element;
return true;
}
return false;
}
delete(element) {
if(this.has(element)) {
delete this.items[element];
return true
}
return false
}
clear() {
this.items = {};
}
has(element) {
return Object.prototype.hasOwnProperty.call(this.items, element);
}
size() {
return Object.keys(this.items).length
}
}
|
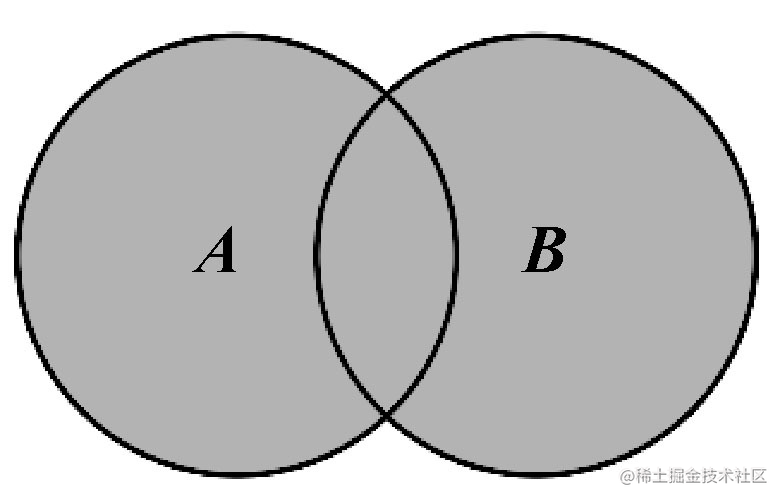
并集 🔗
对于给定的两个集合,返回一个包含两个集合中所有元素的新集合。
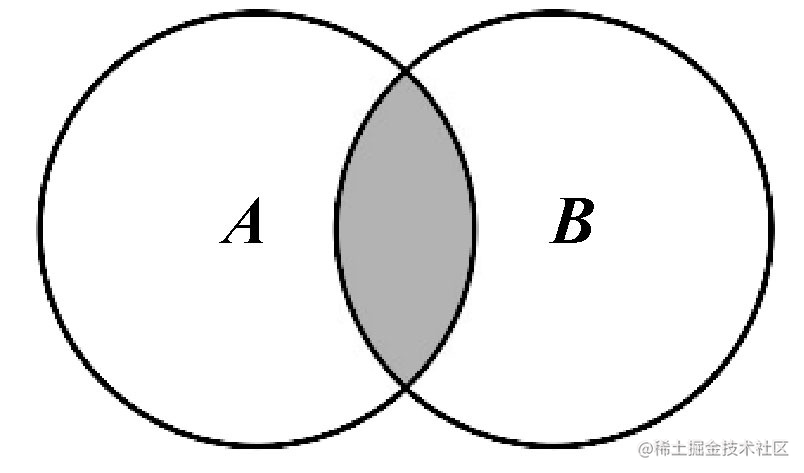
交集 🔗
对于给定的两个集合,返回一个包含两个集合中共有元素的新集合。
差集 🔗
对于给定的两个集合,返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合。
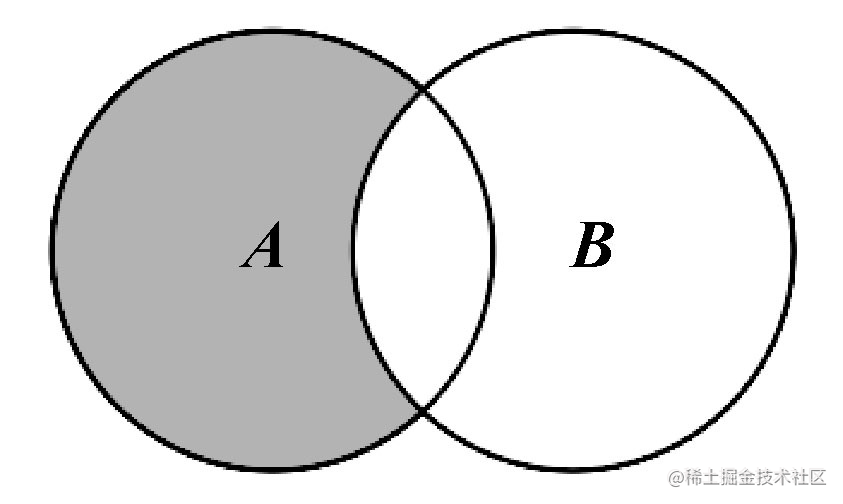
子集 🔗
验证一个给定集合是否是另一集合的子集。

递归 🔗
每个递归函数都必须有基线条件,即一个不再递归调用的条件(停止点),以防止无限递归。
调用栈 🔗
每当一个函数被一个算法调用时,该函数会进入调用栈的顶部。当使用递归的时候,每个函数调用都会堆叠在调用栈的顶部,这是因为每个调用都可能依赖前一个调用的结果。
尾调用优化 🔗
ECMAScript 2015中, 如果函数内的最后一个操作是调用函数(就像示例中加粗的那行),会通过“跳转指令”(jump) 而不是**“子程序调用”(subroutinecall)**来控制。
迭代和递归优缺点 🔗
迭代的版本比递归的版本快很多,所以这表示递归更慢。但是,再看看三个不同版本的代码。递归版本更容易理解,需要的代码通常也更少。
树是一种分层数据的抽象模型。
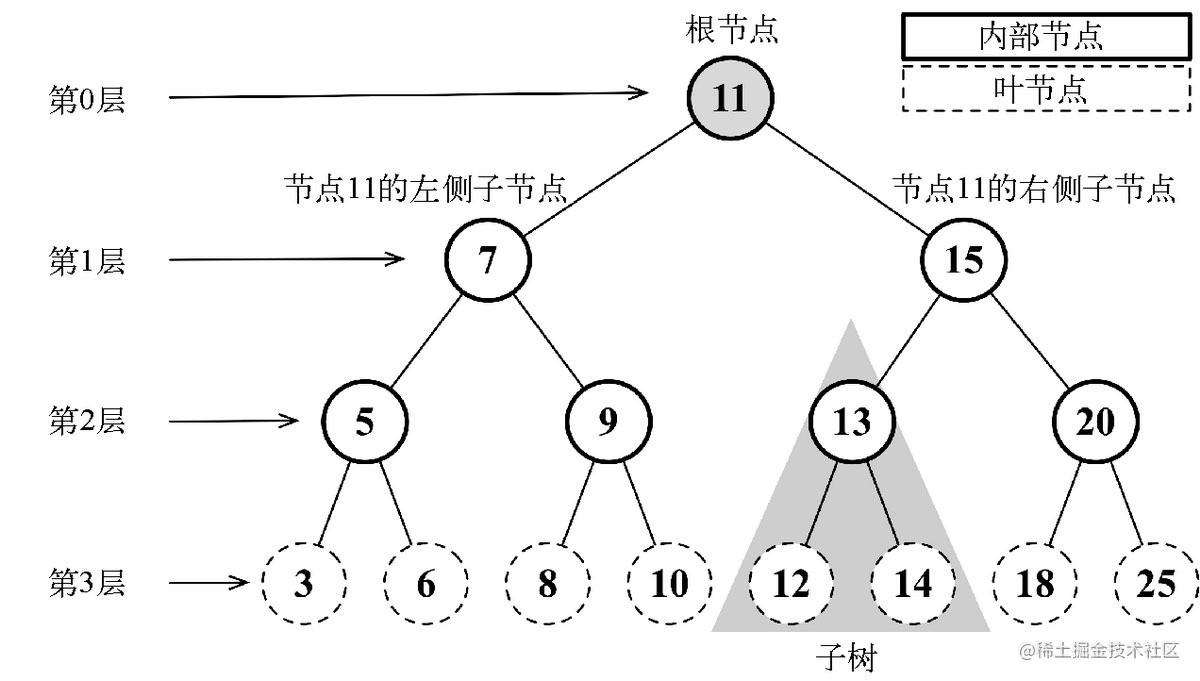
一个节点可以有祖先和后代。
二叉树和二叉搜索树 🔗
二叉树中的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧子节点。
二叉搜索树(Binary Search Tree)(BST)是二叉树的一种,但是只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class BST {
root: any;
compareFn: Function;
constructor(compareFn) {
this.root = null;
this.compareFn = compareFn;
}
insert(key) {
if (this.root == null) {
this.root = new BSTNode(key);
} else {
this.insertNode(this.root, key);
}
}
insertNode(node, key) {
if (this.compareFn(key, node.key)) {
if (node.left == null) {
node.left = new BSTNode(key);
} else {
this.insertNode(node.left, key);
}
} else {
if (node.right == null) {
node.right = new BSTNode(key);
} else {
this.insertNode(node.right, key);
}
}
}
}
class BSTNode {
key: any;
left: BSTNode | null;
right: BSTNode | null;
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}
|
树的遍历 🔗
中序遍历 🔗
中序遍历是一种以上行顺序访问BST所有节点的遍历方式,也就是以从最小到最大的顺序访问所有节点
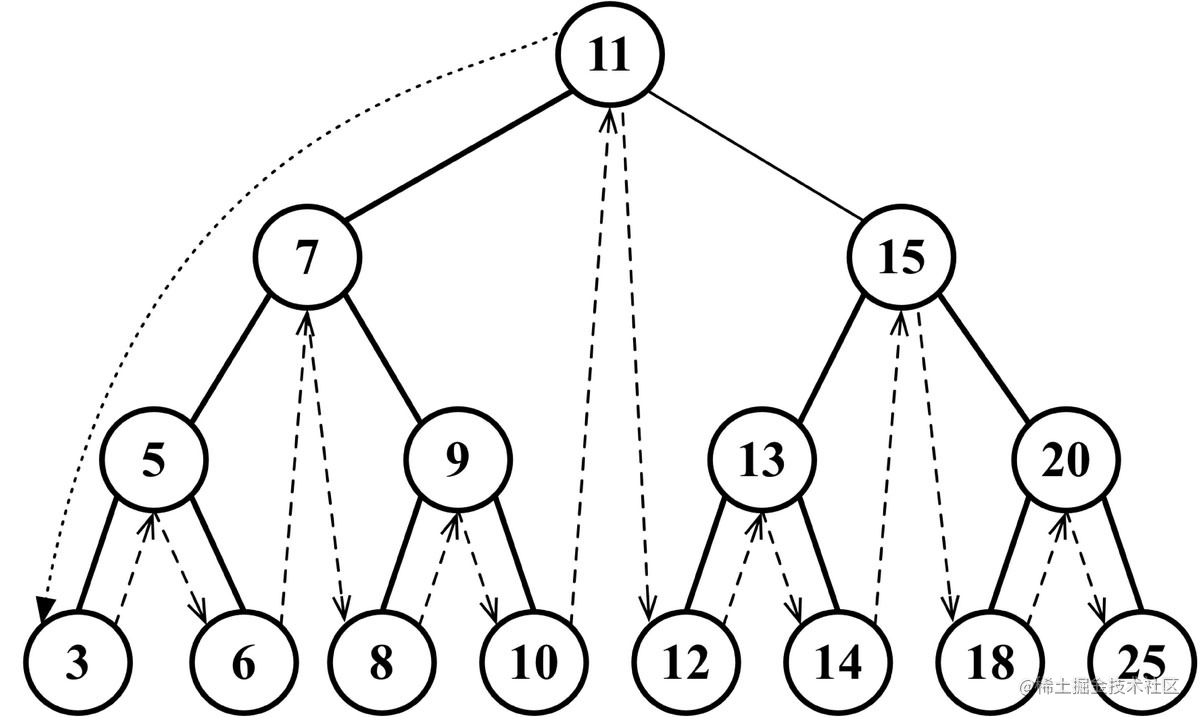
先序遍历 🔗
先序遍历是以优先于后代节点的顺序访问每个节点的
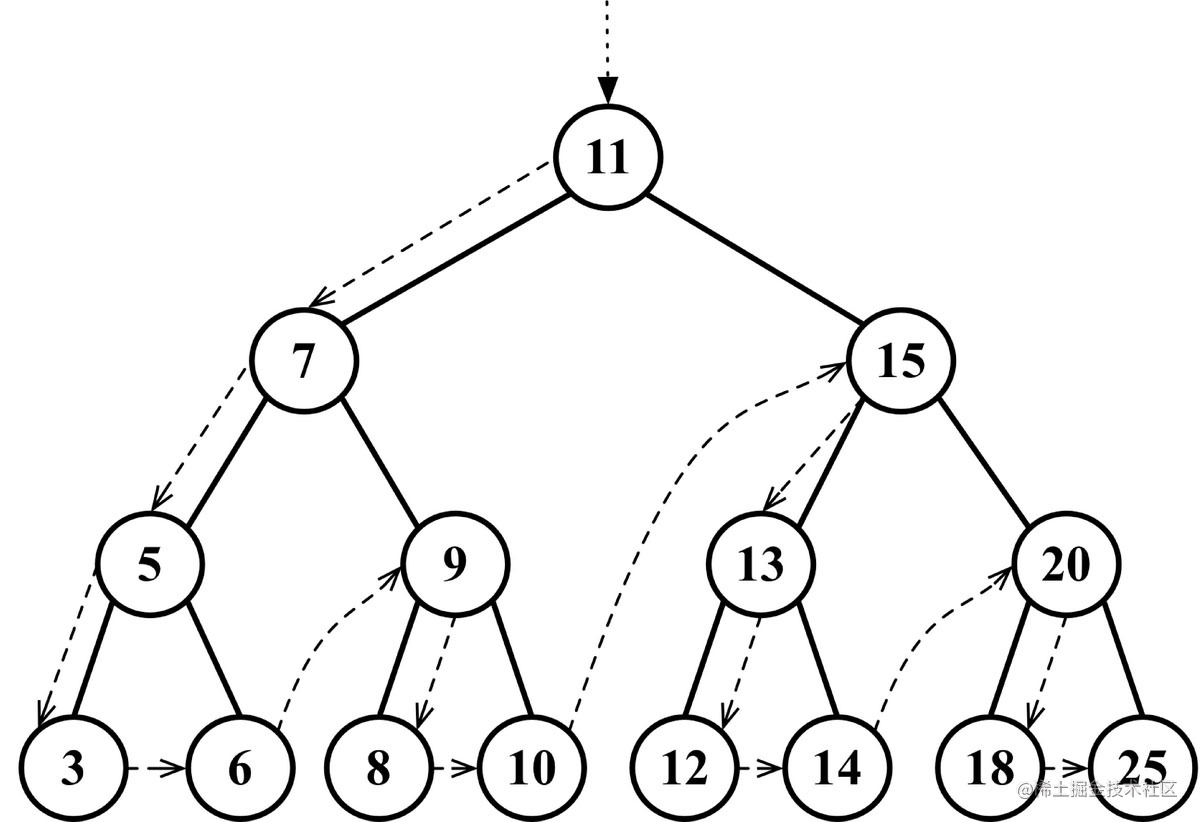
后序遍历 🔗
后序遍历则是先访问节点的后代节点,再访问节点本身。后序遍历的一种应用是计算一个目录及其子目录中所有文件所占空间的大小。
最小值 🔗
树最后一层最左侧的节点,这是这棵树中最小的键
1
2
3
4
5
6
7
| minNode(node) {
let current = node
while(current != null && current.left != null) {
current = current.left
}
return current
}
|
最大值 🔗
树最右端的节点(同样是树的最后一层),这是这棵树中最大的键
1
2
3
4
5
6
7
| maxNode (node) {
let current = node;
while (current != null && current.right != null) {
current = current.right;
}
return current;
}
|
红黑树 🔗
红黑树也是一个自平衡二叉搜索树。
- 顾名思义,每个节点不是红的就是黑的;
- 树的根节点是黑的;
- 所有叶节点都是黑的(用NULL引用表示的节点);
- 如果一个节点是红的,那么它的两个子节点都是黑的;
- 不能有两个相邻的红节点,一个红节点不能有红的父节点或子节点;
- 从给定的节点到它的后代节点(NULL叶节点)的所有路径包含相同数量的黑色节点。
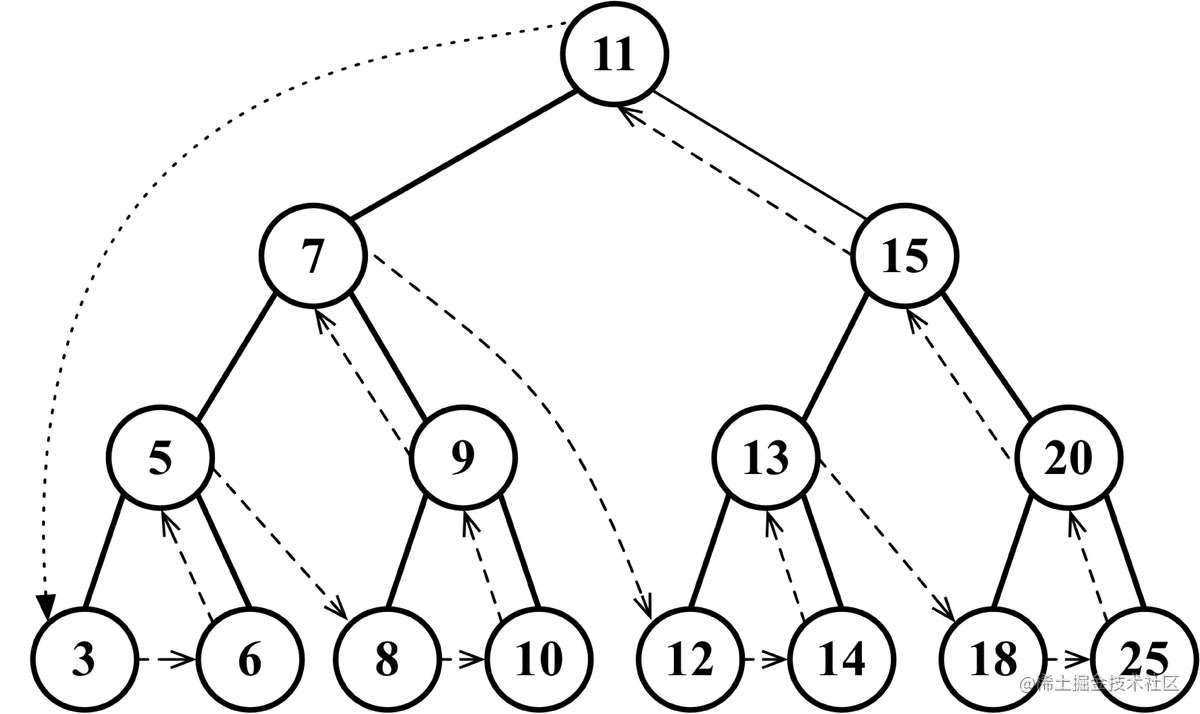
二叉堆和堆排序 🔗
它是一棵完全二叉树,表示树的每一层都有左侧和右侧子节点(除了最后一层的叶节点),并且最后一层的叶节点尽可能都是左侧子节点,这叫作结构特性。
二叉堆不是最小堆就是最大堆。最小堆允许你快速导出树的最小值,最大堆允许你快速导出树的最大值。
尽管二叉堆是二叉树,但并不一定是二叉搜索树(BST)
在二叉堆中,每个子节点都要大于等于父节点(最小堆)或小于等于父节点(最大堆)
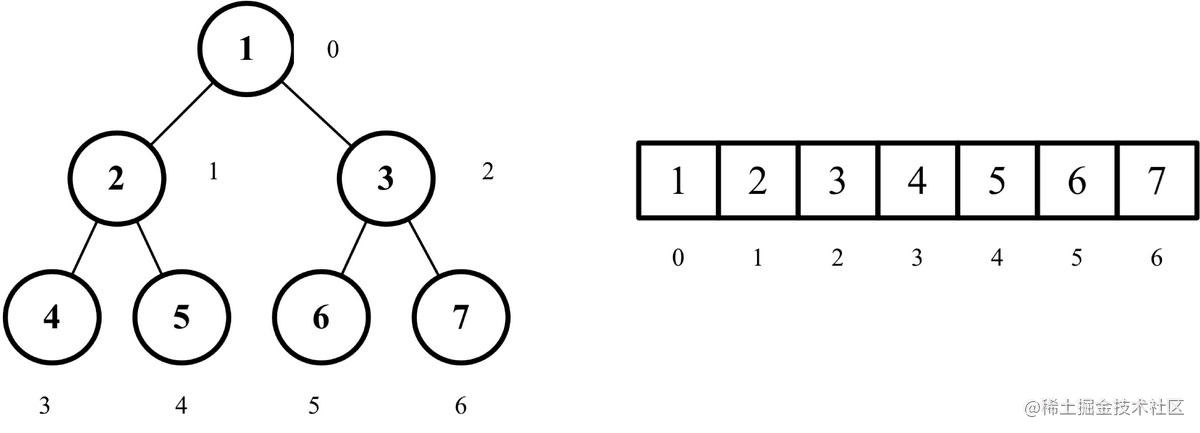
- 它的左侧子节点的位置是2 * index + 1(如果位置可用
- 它的右侧子节点的位置是2 * index + 2(如果位置可用)
- 它的父节点位置是index / 2(如果位置可用)
堆排序算法 🔗
- 用数组创建一个最大堆用作源数据。
- 在创建最大堆后,最大的值会被存储在堆的第一个位置。我们要将它替换为堆的最后一个值,将堆的大小减1。
- 最后,我们将堆的根节点下移并重复步骤2直到堆的大小为1。
